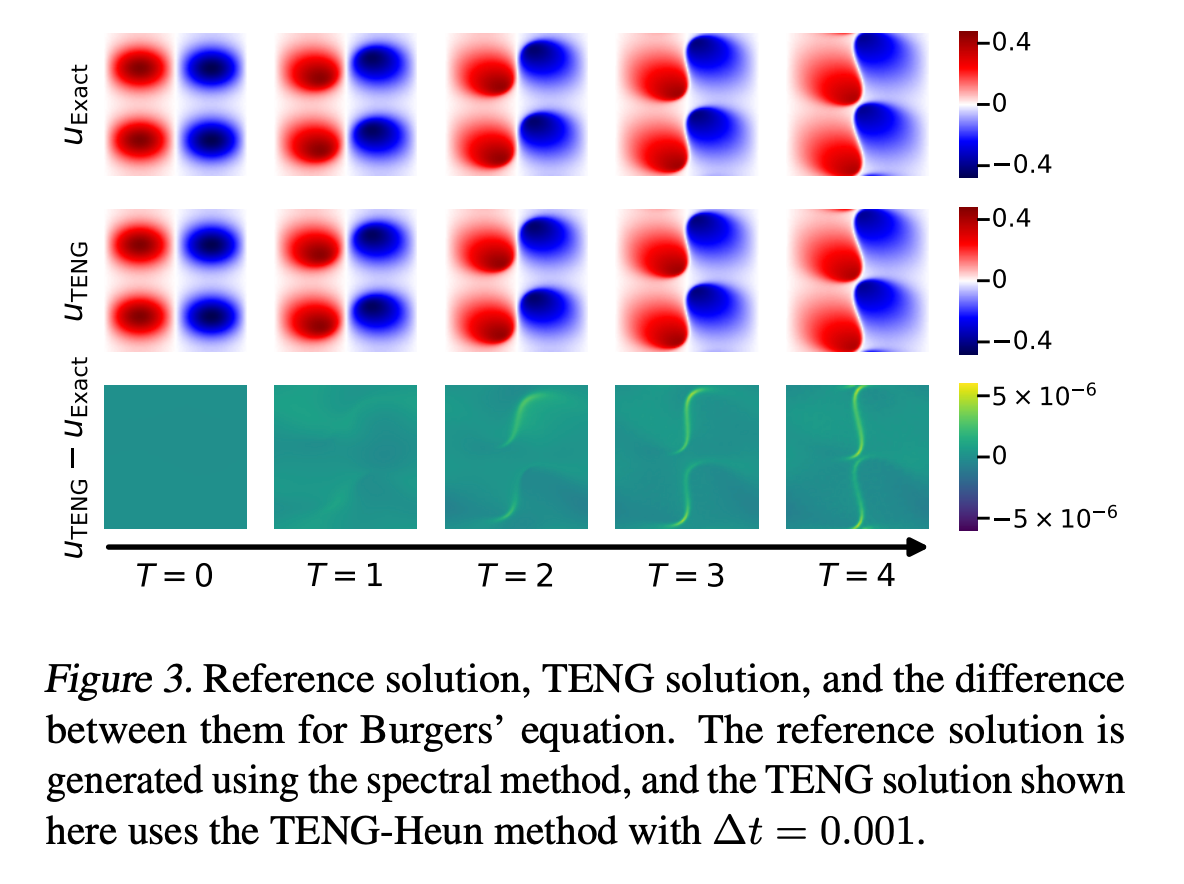
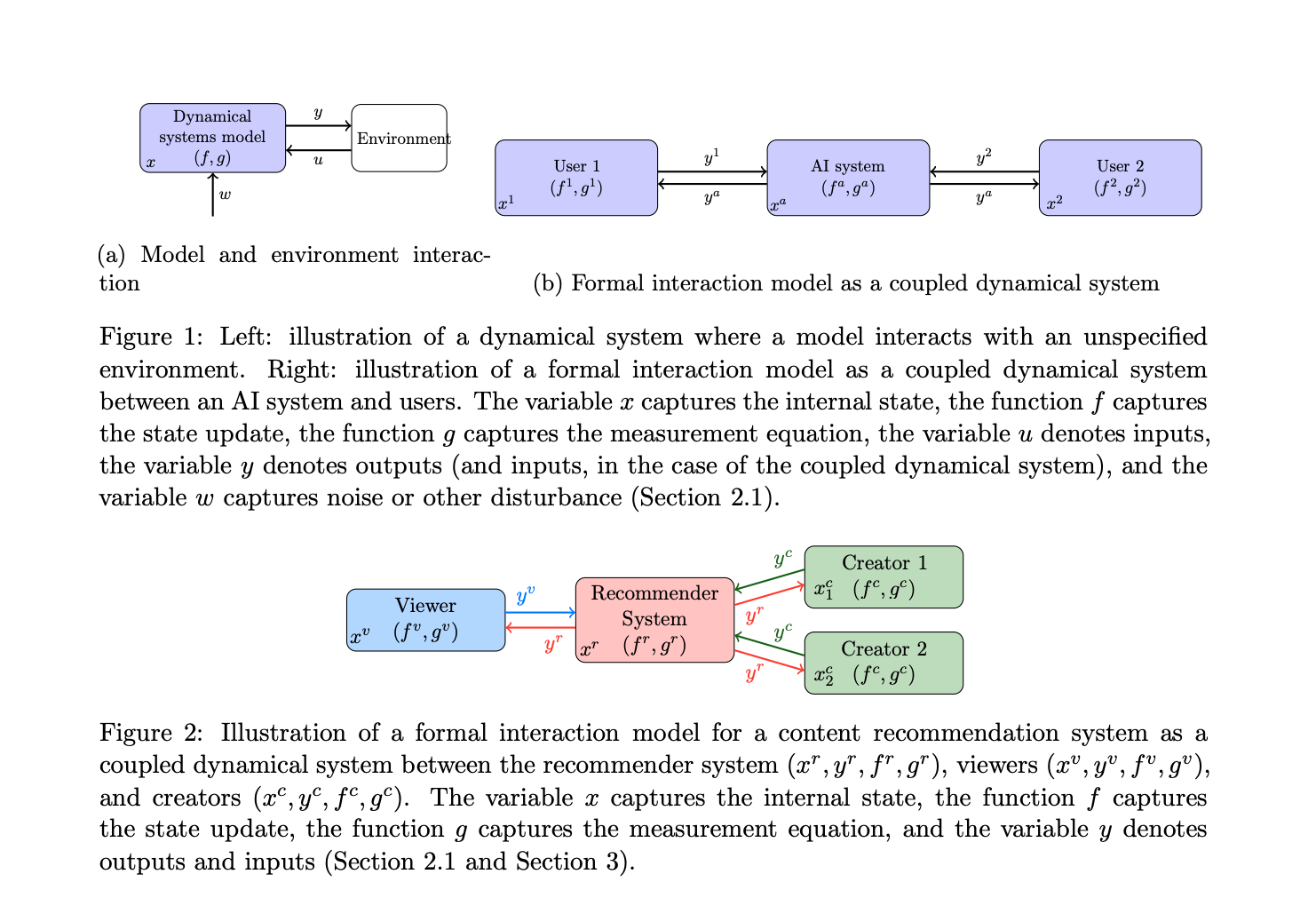
A Comprehensive Analytical Framework for Mathematical Reasoning in Multimodal Large Language Models

Mathematical reasoning has emerged as a critical frontier in artificial intelligence, particularly in developing Large Language Models (LLMs) capable of performing complex problem-solving tasks. While traditional mathematical reasoning focuses on text-based inputs, modern applications increasingly involve multimodal elements including diagrams, graphs, and equations. This presents significant challenges for existing systems in processing and integrating information across different modalities. The complexities extend beyond simple text comprehension, like deep semantic understanding, context preservation across modalities, and the ability to perform complex reasoning tasks combining visual and textual elements.
Since 2021, there has been a steady increase in math-specific Large Language Models (MathLLMs), each addressing different aspects of mathematical problem-solving. Early models like GPT-f and Minerva established foundational capabilities in mathematical reasoning, while Hypertree Proof Search and Jiuzhang 1.0 advanced theorem proving and question understanding. The field further diversified in 2023 by introducing multimodal support through models like SkyworkMath, followed by specialized developments in 2024 focusing on mathematical instruction (Qwen2.5-Math) and proof capabilities (DeepSeek-Proof). Despite these advancements, existing approaches focus too narrowly on specific mathematical domains or fail to address the challenges of multimodal mathematical reasoning.
Researchers from HKUST (GZ), HKUST, NTU, and Squirrel AI have proposed a comprehensive analytical framework to understand the landscape of mathematical reasoning in the context of multimodal large language models (MLLMs). Researchers reviewed over 200 research papers published since 2021, focusing on the emergence and evolution of Math-LLMs in multimodal environments. This systematic approach examines the multimodal mathematical reasoning pipeline while investigating the role of both traditional LLMs and MLLMs. The research particularly emphasizes the identification and analysis of five major challenges that affects the achievement of artificial general intelligence in mathematical reasoning.
The basic architecture focuses on problem-solving scenarios where the input consists of problem statements presented either in pure textual format or accompanied by visual elements such as figures and diagrams. The system processes these inputs to generate solutions in numerical or symbolic formats. While English dominates the available benchmarks, some datasets exist in other languages like Chinese and Romanian. Dataset sizes vary significantly, ranging from compact collections like QRData with 411 questions to extensive repositories like OpenMathInstruct-1 containing 1.8 million problem-solution pairs.
The evaluation of mathematical reasoning capabilities in MLLMs uses two primary approaches: discriminative and generative evaluation methods. In discriminative evaluation, models are evaluated based on their ability to correctly classify or select answers, with advanced metrics like performance drop rate (PDR), and specialized metrics like error step accuracy. The generative evaluation approach focuses on the model’s capacity to produce detailed explanations and step-by-step solutions. Notable frameworks like MathVerse utilize GPT-4 to evaluate the reasoning process, while CHAMP implements a solution evaluation pipeline where GPT-4 serves as a grader comparing generated answers against ground truth solutions.
Here are the five key challenges in mathematical reasoning with MLLMs:
- Visual Reasoning Limitations: Current models struggle with complex visual elements like 3D geometry and irregular tables.
- Limited Multimodal Integration: While models handle text and vision, they cannot process other modalities like audio explanations or interactive simulations.
- Domain Generalization Issues: Models that excel in one mathematical domain often fail to perform well in others, limiting their practical utility.
- Error Detection and Feedback: MLLMs currently lack robust mechanisms to detect, categorize, and correct mathematical errors effectively.
- Educational Integration Challenges: Current systems don’t adequately account for real-world educational elements like handwritten notes and draft work.
In conclusion, researchers presented a comprehensive analysis of mathematical reasoning in MLLMs, that reveals significant progress and persistent challenges in the field. The emergence of specialized Math-LLMs has shown substantial advancement in handling complex mathematical tasks, particularly in multimodal environments. Moreover, addressing the above five challenges is crucial for developing more sophisticated AI systems capable of human-like mathematical reasoning. The insights from this analysis provide a roadmap for future research directions, highlighting the importance of more robust and versatile models that can effectively handle the complexities of mathematical reasoning.
Check out the Paper. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter and join our Telegram Channel and LinkedIn Group. Don’t Forget to join our 60k+ ML SubReddit.
Sajjad Ansari is a final year undergraduate from IIT Kharagpur. As a Tech enthusiast, he delves into the practical applications of AI with a focus on understanding the impact of AI technologies and their real-world implications. He aims to articulate complex AI concepts in a clear and accessible manner.